La sustitución trigonométrica es un método de integración. En lugar de sustituir usando una nueva variable que es función de x (u=f(x)), se define a x como una función trigonométrica de una nueva variable (x=f(θ)).
El método consiste en:
- Reescribir la ecuación en términos de la variable (θ) y su diferencial (dθ)
- Resolver la integral
- Reescribir el resultado en términos de x
Sirve para los siguientes casos:
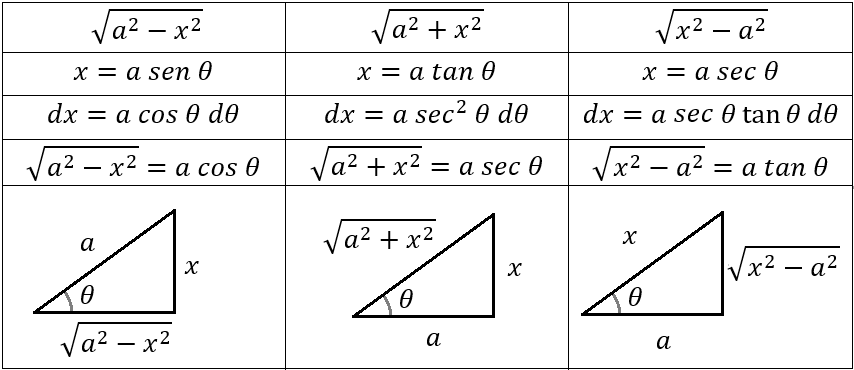
En la tabla se muestra como se deben sustituir la variable x y el diferencial dx.
Después de realizar la integración es recomendable dibujar un triangulo rectángulo en donde se relacionen x, a y θ para regresar la función a términos de x.
Ejemplo:
Hallar la siguiente integral usando el método de sustitución trigonométrica:
A) y= √(a2-x2) / x2
x= a sen θ dx= a cos θ dθ

