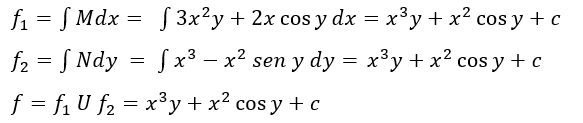Un factor integrante μ (x, y) es un elemento que se usa para multiplicar ambos lados de la ecuación y facilitar su resolución.
Si una ecuación diferencial no exacta es de la siguiente forma
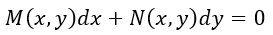
Deberemos usar cualquiera de los factores integrantes que se muestran a continuación para convertir a la ecuación en una ecuación diferencial exacta

El método de resolución consiste en:
- Hallar el factor de integrante
- Multiplicar la ecuación diferencial por el factor de integración
- Hallar la función f (x, y)
- Despejar la variable dependiente
Ejemplo:
Hallar la solución de la ecuación diferencial
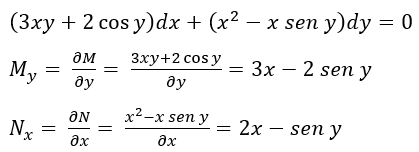
La ecuación diferencial no es exacta
Hallar el factor de integración
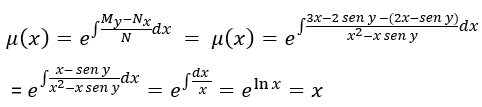
Multiplicar la ecuación diferencial por el factor de integrante
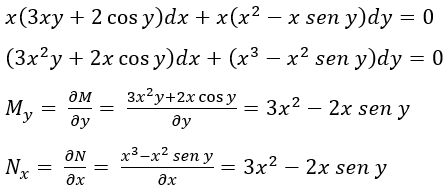
La ecuación diferencial ya es exacta
Hallar la función f (x, y)