Resistencias En Serie Y Paralelo

Las Resistencias son elementos pasivos de la electrónica, quiere decir, que son componentes sin polaridad, por lo tanto, no importa la dirección en la que se coloque una resistencia en un circuito, lo que si importa es la potencia que puede disipar y el valor de su resistencia. La unidad principal para la resistencia son los ohms (Ω). Al incluir varias resistencias en un circuito, dependiendo su configuración será la resistencia equivalente de un circuito. Existen 2 configuraciones principalmente: En Serie y En Paralelo.

Resistencias en Serie

Son las resistencias que comparten un solo nodo en todo el circuito y la resistencia equivalente entre ellas se calcula matemáticamente [Fig.1] y su configuración [Fig.2] de la siguiente manera:

[Fig.1] Expresión para resistencia total o equivalente de resistencias en serie

[Fig.2] Configuración gráfica de resistencias en serie

Resistencias en Paralelo

Son las resistencias que comparten ambos nodos en el circuito y la resistencia equivalente entre ellas se calcula matemáticamente [Fig.3] y su configuración [Fig.4] de la siguiente manera:

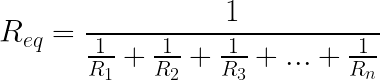
[Fig.3] Expresión para resistencia total o equivalente de resistencias en paralelo
[Fig.4] Configuración gráfica de resistencias en paralelo

Ejemplo:

Calcule la resistencia equivalente Req del circuito del siguiente circuito [Fig.5]:

[Fig.5] Circuito a Resolver

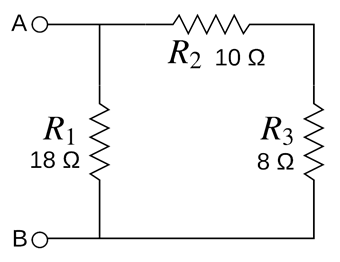
Para determinar el valor de la Resistencia equivalente Req, necesitamos ubicar los puntos de referencia A y B, y empezar a reducir del lado contrario a esos puntos.

Ya que los puntos de referencia A y B están del lado izquierdo, empezamos a reducir del lado derecho.

La primera reducción del circuito será encontrar la resistencia de R2 y R3, ya que, al compartir solo un nodo, las resistencias están en serie, y según la ecuación para encontrar la resistencia [Fig.1] entre ambas debemos sumar algebraicamente sus valores.

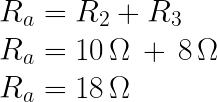
Y el diagrama también queda reducido de la siguiente forma [Fig.6]:

[Fig.6] Circuito Reducido

Una vez reducido el circuito, se tiene otro circuito equivalente con una resistencia Ra en lugar de R2 y R3, para seguir reduciendo el circuito se ve que R1 y Ra comparten ambos nodos, por lo tanto, están en paralelo y utilizando la ecuación para las resistencias en paralelo [Fig.3], la resistencia equivalente será el inverso de la suma de los inversos de R1 y Ra.

Y el diagrama final queda de la siguiente manera [Fig.7]:

[Fig.7] Circuito Resuelto

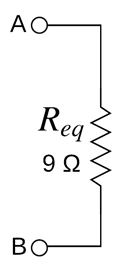
Finalmente se obtiene que la Resistencia equivalente Req, del circuito es igual a 9 Ω, siendo esta resistencia una equivalencia ideal de todas las resistencias del circuito original.