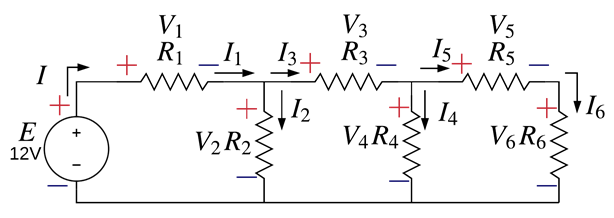
Un circuito en escalera es un circuito que está compuesto generalmente por una fuente de voltaje y un arreglo de resistencias en serie y paralelo (mixto) que hacen que sea un ejercicio muy práctico para aumentar las habilidades del análisis de circuitos. Un circuito en escalera es parecido a la siguiente representación [Fig.1].

Para resolver este tipo de circuitos existen 2 métodos: El gráfico y el Analítico
- Hallar la resistencia total calculando resistencias equivalentes en serie y paralelo, partiendo desde el extremo contrario a la fuente de voltaje.
- Hallar la corriente total.
- Deshacer la reducción del circuito paso por paso en orden inverso a la reducción, calculando los valores de voltaje y corriente en cada resistencia (Utilizando ley de ohm o utilizando divisores de voltaje y corriente).
Método Analítico
- Hallar la corriente de la última rama y dejarla en función de una variable In.
- Expresar cada voltaje y corriente de todas las ramas en función de la corriente In, hasta llegar a la fuente y poder determinar la corriente de la última rama.
- Cualquier valor de voltaje o corriente de una resistencia puede hallarse con facilidad debido a que ya estaba expresado en función de la última corriente In.
Ejemplo:
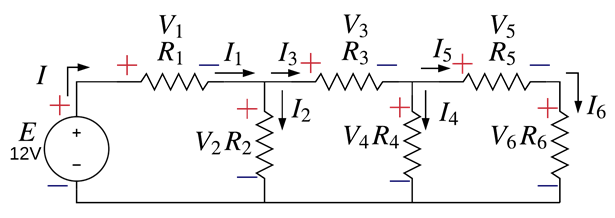
Complete la Tabla [Tab.1]. Calcule I, Req y los voltajes y corrientes que pasan por cada una de las resistencias del siguiente circuito [Fig.2].

Método Gráfico
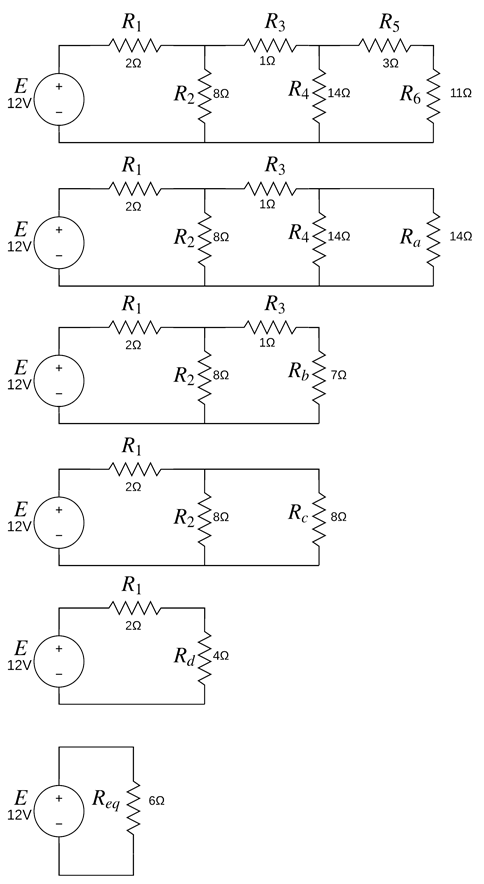
(1) Reducimos el circuito para encontrar Req [Fig.3].
En la primera reducción del circuito se obtiene la primera resistencia equivalente Ra, dado que R5 está en serie con R6, Ra se calcula de la siguiente manera:
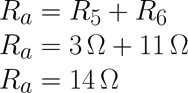
En la segunda reducción del circuito se obtiene la segunda resistencia equivalente Rb, dado que R4 está en paralelo con Ra, Rb se calcula de la siguiente manera:
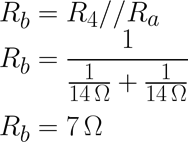
En la tercera reducción del circuito se obtiene la tercera resistencia equivalente Rc, dado que R3 está en serie con Rb, Rc se calcula de la siguiente manera:
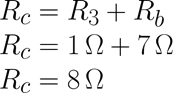
En la cuarta reducción del circuito se obtiene la cuarta resistencia equivalente Rd, dado que R2 está en paralelo con Rc, Rd se calcula de la siguiente manera:
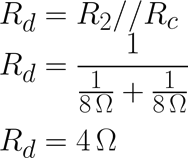
En la quinta reducción del circuito se obtiene la última resistencia equivalente Req, dado que R1 está en serie con Rd, Re se calcula de la siguiente manera:
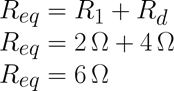
Y se obtiene que Req es igual a 6 Ω
(2) Utilizando la Ley de Ohm para calcular la corriente se tiene que:
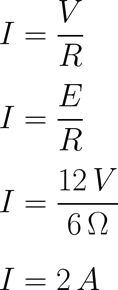
La corriente total del circuito I es de 2 A.
(3) Una vez conociendo Req y I podemos deshacer la reducción calculando voltajes y corrientes.
Expandimos Req y obtenemos los voltajes y corrientes utilizando la ley de ohm, así como se muestra a continuación:
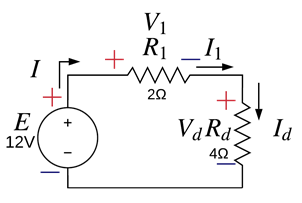
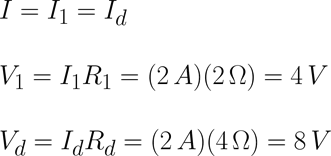
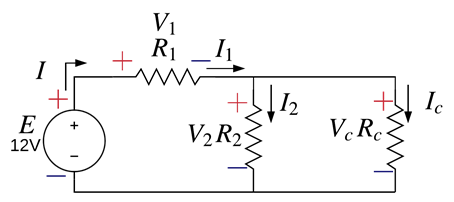
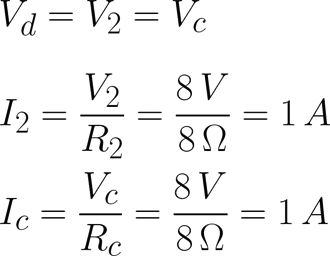
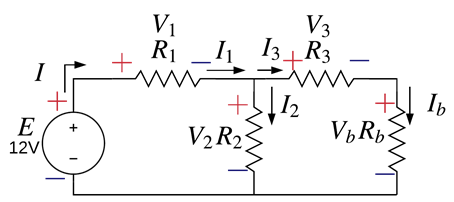
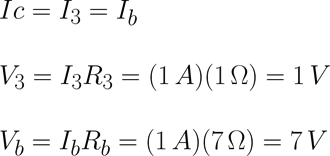
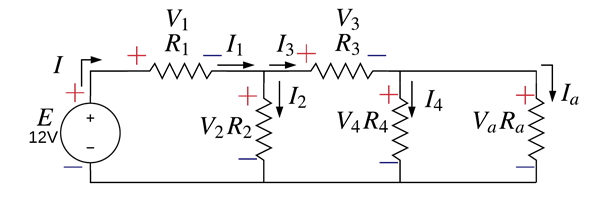
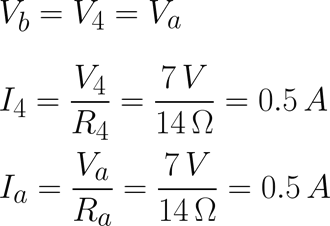
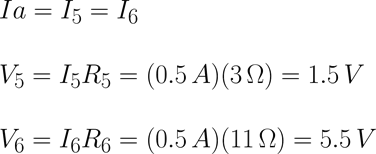
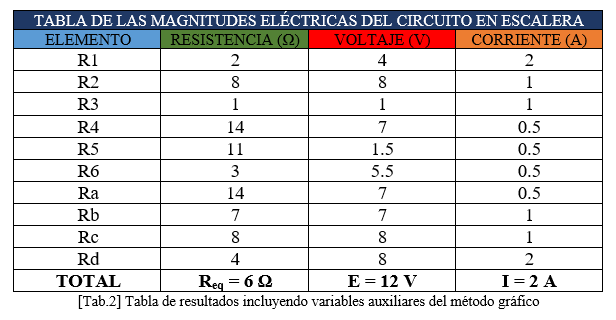
Regresando al circuito original ya se debió de haber calculado las corrientes y voltajes de cada una de las resistencias y llenando la siguiente tabla [Tab.2] que incluye las resistencias equivalentes que fueron auxiliares en este proceso queda de la siguiente manera.
Método Analítico
Siguiendo las instrucciones del método descrito al inicio, vamos a poner todas las ecuaciones en función de I6 y encontrar I6. Conociendo el valor de I6 y con todas las ecuaciones expresadas en términos I6 sustituimos los datos y llenamos la tabla con los resultados [Tab.3].
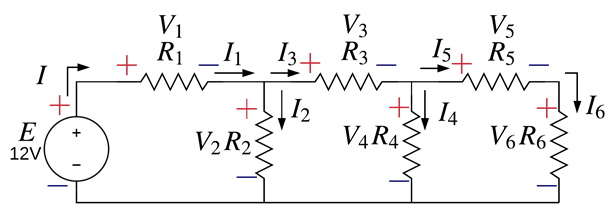
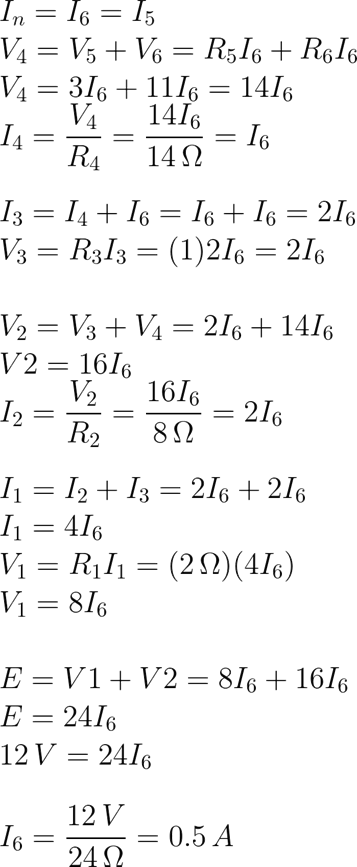
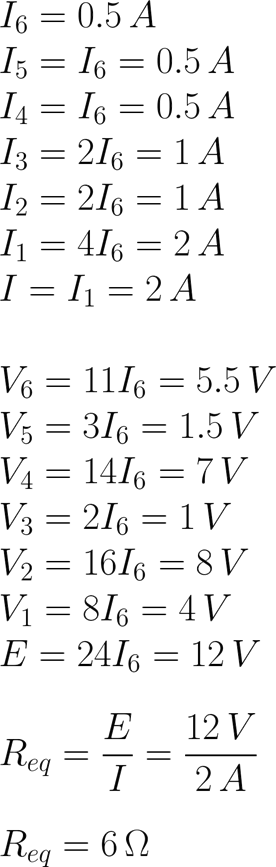
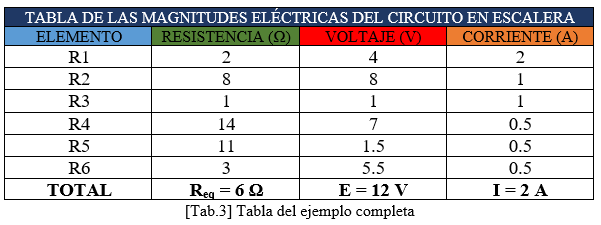
El circuito está resuelto.
