Los límites son valores hacia los que tiende una función cuando se evalúa muy cerca de un valor.
El límite (L) es el valor al que tiende una función (f(x)) cuando la variable independiente (x) se aproxima a un valor(a):
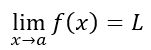
La ecuación anterior se lee como: el límite de f(x) cuando x tiende hacia a es L
Un límite solamente está definido si los límites laterales por la derecha y por la izquierda son iguales.
- Límite por la izquierda: el valor al que tiende la función cuando se aproxima a ese punto desde un valor más pequeño (-) de x.
- Límite por la derecha: el valor al que tiende la función cuando se aproxima a ese punto desde un valor más grande (+) de x.
Continuidad
Una función es continua en un punto si:
- Está definida en ese punto.
- Existe un límite en ese punto.
- El valor de la función es igual al valor del límite.
Una función es continua en un intervalo si es continua en cada uno de los puntos.
Ejemplos:
Hallar el límite, los límites derecho e izquierdo de las siguientes funciones en x=0 y definir si son continuas en ese punto.
A) y=1/x
Los limites por la derecha e izquierda son:
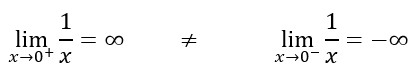
Como los limites laterales son distintos no existe el límite en ese punto. Además, la función no está definida en x=0. Podemos concluir que la función no es continua en ese punto.
B) y=1/x2
Los limites por la derecha e izquierda son:
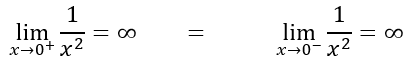
Los límites laterales son iguales en ese punto por lo que el límite existe y su valor es igual al de los limites laterales. Pero la función no está definida en x=0 por lo que a pesar de que existe el límite la función no es continua en ese punto.
