La optimización busca la mejor forma de realizar un proceso o resolver un problema. La optimización está estrechamente ligada con los máximos y mínimos de una función.
Para poder realizar optimización usando derivadas debemos:
- Expresar el problema en forma de ecuación despejada para la variable a optimizar.
- Expresar la ecuación usando solamente una variable independiente. Sustituyendo las demás mediante relaciones establecidas por el problema.
- Buscar los máximos o mínimos de la función.
Ejemplo:
Se va a construir una cerca a un costado de un rio por lo que solamente serán necesarios tres lados de cerca. Hallar el área máxima y las dimensiones óptimas para maximizar el área de superficie cercada considerando que se pueden construir solamente 1000 metros de cerca.
Procedimiento:
Hacer un diagrama
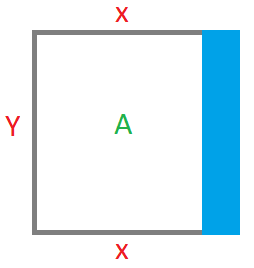
Expresar el problema en forma de ecuación:
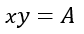
Expresar la ecuación usando solamente una variable independiente. Utilizando la relación dada por las condiciones del problema y sustituyendo en la ecuación:
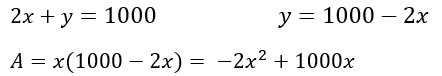
Buscar el máximo de la función.
Hallar primera y segunda derivada:
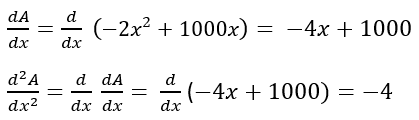
Buscar los valores de x para los que la derivada es cero:

Solamente existe un valor posible y es un máximo debido a que la segunda derivada es igual a -4.
Para hallar las dimensiones debemos sustituir x en la ecuación despejada de y:
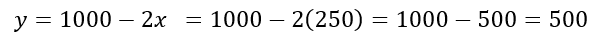
El área es:
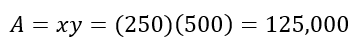
Las dimensiones óptimas para maximizar el área cercada son y=500 y x=250. El área máxima que se puede cercar es A =125,000 metros cuadrados.
