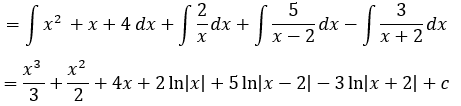El método de integración por fracciones parciales sirve para integrar una función que sea una división de polinomios. El resultado es una suma de fracciones más simples llamadas fracciones parciales.
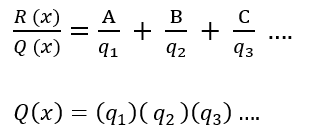
El método consiste en:
- Comprobar que el grado de R sea menor al grado de Q. Si no es así debemos hacer división de polinomios.
- Una vez que el grado de R sea menor factorizar Q
- Expresar la función como suma de coeficientes entre factores de Q (si hay un factor repetido se escribirá una segunda vez, pero elevado al cuadrado)
- Hallar los coeficientes
- Integrar las fracciones parciales
Ejemplo:
Hallar las siguientes integrales usando el método de fracciones parciales:
A) y= (2x-1) / (x2-3x+2)
El grado de R es menor así que no es necesario realizar división de polinomios.
Realizar la factorización y expresar la función como suma de coeficientes entre factores de Q:
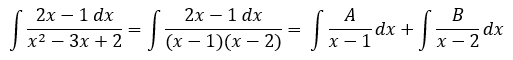
Hallar los coeficientes:
Para hallar un coeficiente debemos evaluar la función original en el valor de x que permite hacer cero a ese factor de Q y eliminando ese factor de la ecuación.
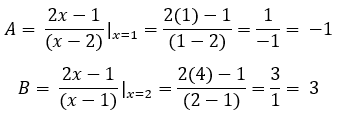
Integrar las fracciones parciales:
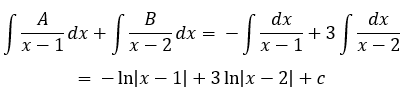
B) y= (x5+ x4-8) / (x3-4x)
El grado de R es mayor así que es necesario realizar división de polinomios.
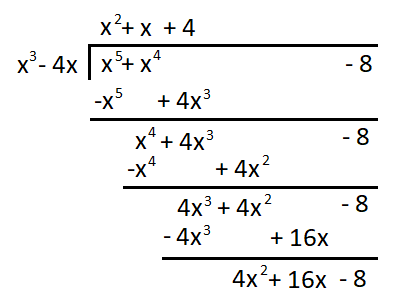
Realizar la factorización y expresar la función como suma de coeficientes entre factores de Q:
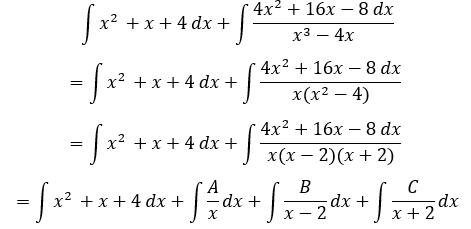
Hallar los coeficientes:
Para hallar un coeficiente debemos evaluar la función original en el valor de x que permite hacer cero a ese factor de Q y eliminando ese factor de la ecuación.

Integrar las fracciones parciales: