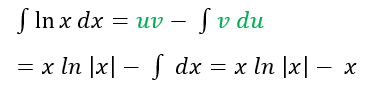El método de integración por partes es equivalente a la regla del producto en cálculo diferencial. Sirve para hallar integrales de un producto de funciones.
Partiendo de la regla del producto:
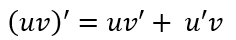
Integramos en ambos lados:
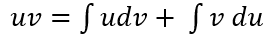
Despejamos una integral y obtenemos la fórmula para integración por partes:

Para determinar u y dv debemos seleccionar como u una función fácilmente derivable (para hallar du) y como dv una función fácilmente integrable (para hallar v). Se recomienda seguir el método ILATE.
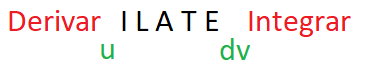
Las funciones más fáciles de integrar son las exponenciales y luego las trigonométricas, algebraicas, logarítmicas y funciones inversas en ese orden.
Ejemplo:
Hallar las siguientes integrales usando el método de integración por partes
A) y= x cos x
u = x du = dx
dv= cos x v=sen
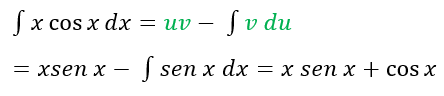
B) y= ln x
u = ln x du = dx/x
dv= dx v=x