Una ecuación diferencial es una ecuación que contiene derivadas de una o más variables dependientes con respecto a una o más variables independientes.
En una ecuación diferencial ordinaria solamente hay una variable independiente.
En una ecuación diferencial parcial hay dos o más variables independientes.
El orden de la ecuación diferencial es el orden de la mayor derivada en la ecuación.
Una ecuación diferencial es lineal si se cumplen las siguientes condiciones:
- La variable dependiente (y) y todas sus derivadas son de primer grado.
- No hay funciones no lineales de la variable dependiente (y)
- Los coeficientes solamente son función de la variable independiente (x).
Una ecuación diferencial lineal de segundo orden tiene la siguiente forma:
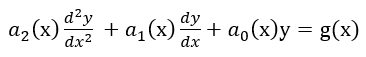
En un problema con valores iniciales (PVI) se dan las condiciones cuando la variable independiente es igual a cero (condiciones iniciales) y en un problema con valores en la frontera (PVF) se dan las condiciones cuando la variable independiente es diferente de cero (condiciones en la frontera).
Tipos de soluciones
- Solución general (o familia de soluciones) contiene constantes indefinidas.
- Solución particular es un caso particular de la solución general en donde las constantes están definidas. El problema debe tener condiciones iniciales o en la frontera.
Ejemplos
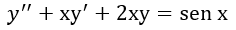
Es una ecuación diferencial lineal de segundo orden

Es una ecuación diferencial no lineal de primer orden
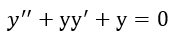
Es una ecuación diferencial no lineal de segundo orden
