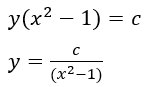Una ecuación diferencial de la forma
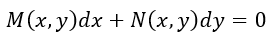
es exacta si se cumple la siguiente condición
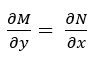
Se dice que la ecuación es una diferencial exacta de una función f (x, y) en donde

Para hallar la función debemos integrar

Después unimos ambos resultados e igualamos la función a una constante debido a que sabemos que su derivada da como resultado cero.
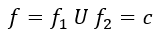
El método de resolución consiste en:
- Comprobar que la ecuación diferencial es exacta
- Hallar la función
- Despejar la variable dependiente
Ejemplo:
Hallar la solución de la ecuación diferencial
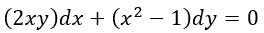
Comprobar que la ecuación diferencial es exacta
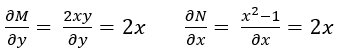
La ecuación diferencial es exacta
Hallar la función
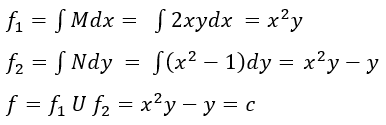
Despejar la variable dependiente