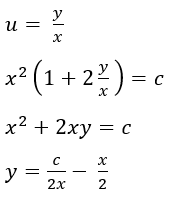Una función es homogénea si al multiplicar todas sus variables por una constante (t) se cumple:

En donde α es el grado de homogeneidad
Una ecuación diferencial de la forma

es homogénea si se cumple que tanto M y N son funciones homogéneas y tienen el mismo grado de homogeneidad.
Existe una definición alternativa para una ecuación diferencial homogénea que se analizará en la sección de coeficientes constantes.
El método de resolución consiste en:
- Comprobar que la ecuación diferencial es homogénea
- Despejar la derivada como función de M y N
- Hacer una sustitución del tipo u=y/x o v=x/y
- Resolver la ecuación diferencial
- Deshacer la sustitución
Ejemplo:
Hallar la solución de la ecuación diferencial

Comprobar que la ecuación diferencial es homogénea
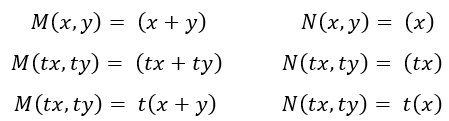
La ecuación diferencial es homogénea debido a que M y N son homogéneas del mismo grado
Despejar la derivada como función de M y N
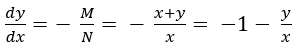
Hacer una sustitución del tipo u=y/x o v=x/y

Resolver la ecuación diferencial

Deshacer la sustitución