Para resolver un sistema de ecuaciones diferenciales de coeficientes constantes con una o más variables dependientes con respecto a una variable dependiente utilizaremos el método de eliminación sistemática
El método consiste en:
- Escribir el sistema empleando el operador diferencial (D=d/dx)
- Despejar una variable dependiente (ej. x) en una ecuación
- Sustituir en la otra ecuación
- Formar una ecuación algebraica en términos del operador diferencial (D)
- Hallar las raíces de la ecuación anterior
- Hallar el valor de la otra variable dependiente (la que no fue despejada ej. y). Es igual a exponenciales elevados a las raíces encontradas en el paso anterior
- Sustituir para hallar el valor de la variable dependiente despejada (ej. x)
Ejemplo
Hallar las soluciones del sistema de ecuaciones diferenciales
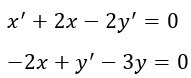
Escribir el sistema empleando el operador diferencial

Despejar una variable dependiente (x)
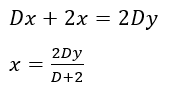
Sustituir en la otra ecuación

Formar una ecuación algebraica en términos del operador (dividimos entre y)

Hallar las raíces
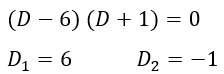
Hallar el valor de la otra variable dependiente (y)

Sustituir para hallar el valor de la variable dependiente despejada (x)
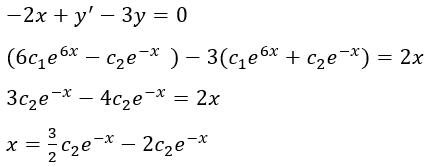
En caso de que al sustituir no lográramos despejar x y nos quedaran derivadas de x tendríamos que resolver la ecuación diferencial.
