El método de variación de parámetros sirve para resolver ecuaciones diferenciales lineales de la forma:
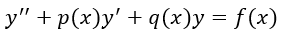
La solución de la ecuación diferencial es
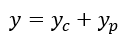
Está formada por la solución complementaria que se calcula aplicando el método de coeficientes constantes a la ecuación homogénea asociada.

Y la solución particular que se calcula usando las funciones auxiliares

En donde W es el Wronskiano de x y y definido por el siguiente determinante:
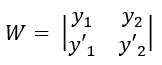
El método consiste en:
- Hallar la solución complementaria usando la educación homogénea asociada y el método de coeficientes constantes
- Hallar el Wronskiano
- Hallar las funciones auxiliares y la solución particular
Ejemplo
Hallar la solución de la ecuación diferencial
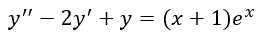
Hallar la solución complementaria
La ecuación diferencial homogénea asociada es:

La ecuación algebraica asociada es:

La solución complementaria es:
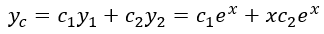
Hallar el Wronskiano
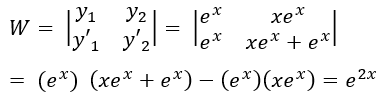
Hallar las funciones auxiliares y la solución particular

